分析千岛湖鸟类多样性与墓群出现率的决定性因素
三墩职业技术学校空想资本主义学院理论想像学研究所, 杭州 310058, 中国浙江
摘要
由于常规的逐步回归分析在使用过程中有诸多缺陷,而信息理论的赤池信息量准则(AIC)弥补了这一缺点。此文基于AIC的判定方法,利用模型选择和多模型推断(model selection and multimodel inference)探讨千岛湖岛屿鸟类多样性的决定因素。同时开展对千岛湖墓葬分布的可能性分析,为盗墓的理论研究打下翔实的基础。
关键词
AIC、盗墓、多模型推断、模型选择、鸟类、千岛湖、逐步回归
前言
面对一系列可能的备选模型,如何评判模型的优劣?选用逐步回归分析(stepwise regression)还是信息理论(information theoretic analysis)?Whittingham等(2006)对2004年的Ecology Letters、Journal of Applied Ecology和Animal Behaviors三个杂志分析,共有65篇文章使用多元回归(multiple regression),其中57%的研究使用了逐步回归的方法。虽然逐步回归依旧广泛使用,但是有许多缺陷,如:参数估计的误差(bias in parameter),模型选择算法的不一致(inconsistencies among model selection algorithms),多个假设检验的内在缺陷(inherent problem of multiple hypothesis testing),以及最后结果只依赖单一的最优模型(inappropriate focus or reliance on a single best model)。至于具体的缺陷原理,此处不予细说,本文将采用信息理论简要介绍多模型推断的方法。
千岛湖地处浙江西部,山清水秀,民风淳朴(此处省略一百字)。自1959年新安江大坝建成后,形成1078个岛屿(108米水位时),乃名副其实的“千岛湖”,是一个得天独厚的路桥岛屿天然实验场所。本研究团队自2003年开始千岛湖地区的鸟类调查,到目前已经逐渐拓展到蜘蛛、蜥蜴、青蛙、蛇、猴子、昆虫、兽类、蝴蝶以及植物等各项业务,欢迎广大生态爱好者和有志之士前来参观与洽谈。撰写本文的起因是早先跟本团队中的“蜘蛛侠”吴博士尝试探讨鸟类多样性与风水的关系,加上近日刚好看了一些有关模型选择和多模型推断(model selection and multimodel inference)的文献(xián),采用“先进”的AIC(Akaike information criterion)技术,探讨该学术问题的可能性。
本文主要探讨的问题包括两部分:1) AIC是啥?莫非是美国国际大学(American International College)的缩写?2) 模型选择的操作步骤;3) 千岛湖岛屿上鸟类和墓葬分布的机理。
材料与方法
研究地点与岛屿参数
按照面积和隔离度,利用分层随机抽样法(stratified random sampling)在千岛湖选取40个岛屿。自2002年开始实地考察并详细并测量了跟鸟类多样性相关的各种岛屿参数:面积、隔离度、 植被物种数、生境种类、周长、周长面积比、形状指数、海拔,并于昨晚想像了各种与盗墓可能相关的岛屿参数:凹凸度、坡度、朝向、铝和硅的含量,沙土指数和pH值。
其中铝和硅的含量是白膏泥的主要组成元素。由于白膏泥防水性能好,是墓葬出没的指标。沙土指数反映了建墓的可能性,即如果沙土含量过多,土质不夯实,容易测漏。pH值,跟墓葬中的有机体“发酵”程度相关。形状指数、凹凸度、坡度和朝向是判断风水优劣的关键,因为圆山、朝南、土层厚及石头少的生境是墓葬出现的高发区。
AIC
AIC(Akaika Information Criterion)即赤池信息量准则,是评估统计模型的复杂度和衡量统计模型拟合优良性的一种标准。最早由日本统计学家赤池弘次创立和发展,由此得名。
AIC在一般情况下,可以表示为
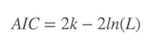
其中: k是参数的数量, L是似然函数(likelihood function)。这是公式,知道就可以,R语言中有现成的命令(stat包中的AIC命令,及stats包中的extractAIC命令)。如果自己动手算,也可以:假设条件是模型的误差服从独立正态分布,n为观察数, RSS为残差平方和,则
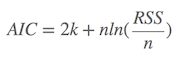
增加了自由参数提高了拟合的优良性,即AIC鼓励数据的优良性但是尽量避免出现过度拟合(overfitting)的情况,所以优先考虑的模型是AIC值最小的那一只。
其中在小样本的情况下(n/k < 40),AIC 转变成AICc (corrected AIC),即:
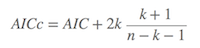
当n增加时,AICc收敛成AIC。所以AICc可以应用于任何样本大小的情况下(注: 这部分内容主要抄自维基百科,不过维基百科的该页中文文献引用有个小错误,即参考书是 Burham & Anderson(2002),而不是2004)
如果数据有过度离散(overdispersion)的影响,则需要考虑Q版的AIC,即
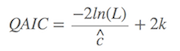
$\hat{c}$ 为方差膨胀系数(VIF)或者过度离散系数(overdispersion coefficient)。如果 $\hat{c}$ 大于1,则需要采用QAIC。当然,Q版的,也有QAICc,道理同上。一般在参数进入模型前,只要保证参数的独立性,则可以避免过度离散的情况。
计算模型权重
得到各个模型的AIC值后,按照AIC从小到大排列,然后每个模型的AIC值与最小的AIC值相减,得到ΔAIC。
通过得到的ΔAIC,计算各个模型的模型权重,即Akaika weight(wi )。其中第 i 个模型的模型权重为:
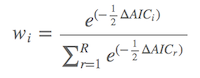
公式不复杂,而且R中有现成的命令计算wi 。wi 在0至1之间,并且所有模型权重之和为1。模型权重越大,表示该模型是真实模型的可能性就越大。比如第二个模型的w2 为0.31,则表示这个模型为真实模型(best possible model)的可能性为31%。
通过模型权重还可以计算各个参数的重要值(importance)。方法很简单,比如参数1,则挑出含参数1的所有模型,然后把这些模型的权重相加,即是该参数的权重。各个参数的权重值一比,就知道哪个参数最重要了。
模型选择的不确定性和多模型推断
其实现实一般不会这么完美的,上述所有结论都建立在ΔAIC>2的基础上,即第二个模型的AIC值比最小模型的AIC值差值大于2。如果小于2,则说明第一个模型跟第二个模型(或者连续前四五个模型)为真实模型的可能性差不多,无法决定优劣。咋么办?终极武器:模型平均(model averaging)。
曾经ΔAIC>2是条金科玉律(Burnham & Anderson, 2002),但是Anderson大神在2008版的书中似乎把ΔAIC>2给降级了(Andersion, 2008),建议不要轻信这条规律,而是建议把所有模型统统进行模型平均,也就是不要随便剔除一些看似不可能模型,哪怕这些模型的权重都小得接近于零。如果ΔAIC>2,通过最优模型,代入实际岛屿参数测量值,就可以计算出预测的鸟类种数或者存在墓葬的可能性。现在由于ΔAIC<2,第一个模型无法“代表”其他模型,于是所有模型都得参与进来。假设 Y^ 值为预测值(鸟类种数或墓葬出现概率),则平均预测值为:
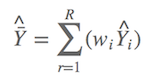
啥意思?假设有九个可能模型,则有九个模型的权重,以及可以计算出九个预测值。如今,平均预测值就是预测值分别乘以权重后的和,比如
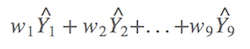
既然预测值Y^需要模型平均,参数估计值也得平均,道理跟估计预测值相似。假设参数i的参数估计为θi,本来当ΔAIC>2时只要直接采用最小AIC模型的 θi 值即可,现在则需要把含有参数 i 的所有模型列出来,进行模型平均:
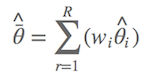
同理,计算参数估计的方差时,也得进行模型平均,得到非条件方差估计(unconditional variance estimate),详见(Burnham & Anderson, 2002, p.162):
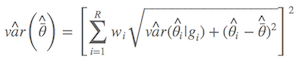
Anderson大神似乎对这个公式也不是很满意,建议更新为Anderson (2008)第111页的公式,其实计算结果相差不多:
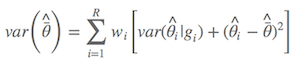
其中 $\hat{\bar{θ}}$ 是模型的平均参数估计,wi 是模型权重,以及 gi 表示第i 个模型。简言之,非条件方差估计就是包括两部分:根号内的前部分是本身的取样方差,另外一部分是由于模型选择不确定导致的方差。所以,把后者考虑进去以后,最后的方差估计不会由于模型的不确定性而降低准确性。我怕表达有所不准,列出Anderson(2008)第111页的原文: an estimator of the variance of parameter estimater esimates that incorporates both sampling variance, given a model, and a variance component for model selection uncertainty. 所以,在样本量较大的前提下,最后参数的置信区间为
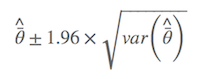
实战演练
演练开始之前,请确保已经安装下列软件包:glmulti, MuMIn, bbmle。网速给力的情况下,最简单的方法是直接在R语言操作界面中输入
install.packages("glmulti")否则,得从R的镜像网站下载压缩包后再本地安装。
演练一:千岛湖鸟类多样性的决定因素
导入 glmulti包
library(glmulti)###Loading required package: rJava
导入千岛湖鸟类和岛屿数据(注:这个数据是真实的,只是我把数据的顺序随机调换了)
tilbird <- read.table("http://sixf.org/files/code/2014/tilbird.txt", h = T) #找到 'tilbird.txt'文件并打开
str(tilbird) ##检查`til.bird`的数据结构###'data.frame': 40 obs. of 9 variables:
### $ birdspp : int 43 34 35 32 31 27 30 33 24 24 ...
### $ area : num 1289.2 143.2 109 55.1 46.4 ...
### $ isolation: num 897 1415 965 954 730 ...
### $ plants : int 36 50 88 86 65 68 45 49 45 31 ...
### $ habitats : int 3 6 3 3 3 3 3 7 4 4 ...
### $ Pe : num 105965 17465 12022 7570 10444 ...
### $ PAR : num 82.2 122 110.3 137.4 225.2 ...
### $ SI : num 832 412 325 288 433 ...
### $ elev : num 298 251 227 198 174 ...
数据中第一列为鸟类物种数,其余八列为岛屿参数,分别为:面积、隔离度、植物物种数、生境类别数、岛屿周长、周长面积比(越大表示边缘越多)、形状指数(完全的圆形,则形状指数为1)和海拔。
模型开始之前得进行岛屿参数的独立性检验。其中方法可以使用相关分析(correlation test),方差膨胀系数(VIF)和主成份分析(PCA),这里采用常用的相关分析。
相关分析的R语言命令是cor.test,这是两两检验。cor是多个参数一起检验,可以多个参数一起检验的时候,结果不给出p值,于是我写了一个小函数,就是多个参数检验的时候也同时给出p值。命令名称为cor.sig,代码为:
cor.sig = function(test) {
res.cor = cor(test)
res.sig = res.cor
res.sig[abs(res.sig) > 0] = NA
nx = dim(test)[2]
for (i in 1:nx) {
for (j in 1:nx) {
res.cor1 = as.numeric(cor.test(test[, i], test[, j])$est)
res.sig1 = as.numeric(cor.test(test[, i], test[, j])$p.value)
if (res.sig1 <= 0.001) {
sig.mark = "***"
}
if (res.sig1 <= 0.01 & res.sig1 > 0.001) {
sig.mark = "** "
}
if (res.sig1 <= 0.05 & res.sig1 > 0.01) {
sig.mark = "* "
}
if (res.sig1 > 0.05) {
sig.mark = " "
}
if (res.cor1 > 0) {
res.sig[i, j] = paste(" ", as.character(round(res.cor1, 3)),
sig.mark, sep = "")
} else {
res.sig[i, j] = paste(as.character(round(res.cor1, 3)), sig.mark,
sep = "")
}
}
}
as.data.frame(res.sig)
}所有岛屿参数进行相关分析,
cor.sig(tilbird[, 2:9]) #第一列不算,那是鸟类物种数,即Y值。### area isolation plants habitats Pe PAR
###area 1*** -0.115 -0.139 -0.064 0.996*** -0.429**
###isolation -0.115 1*** -0.101 -0.1 -0.117 0.299
###plants -0.139 -0.101 1*** -0.16 -0.138 -0.048
###habitats -0.064 -0.1 -0.16 1*** -0.057 -0.035
###Pe 0.996*** -0.117 -0.138 -0.057 1*** -0.481**
###PAR -0.429** 0.299 -0.048 -0.035 -0.481** 1***
###SI 0.857*** -0.045 -0.167 -0.034 0.898*** -0.619***
###elev 0.726*** -0.127 -0.039 -0.032 0.775*** -0.803***
### SI elev
###area 0.857*** 0.726***
###isolation -0.045 -0.127
###plants -0.167 -0.039
###habitats -0.034 -0.032
###Pe 0.898*** 0.775***
###PAR -0.619*** -0.803***
###SI 1*** 0.888***
###elev 0.888*** 1***
结果表明,面积跟周长、周长面积比、形状指数和海拔呈显著相关。考虑到这些因素的生物学意义,很明显,除去其他显著相关的参数而保留面积是合理的,因为在岛屿生物地理学框架下,面积是极为重要的参数,且这里的其他参数都可能由于面积而产生。比如海拔,由于是岛屿,在坡度相似的情况下,面积越大,海拔越高。所以,最后进入模型的是四个参数:面积、隔离度、植物数和生境数。
权且采用最常见的线性模型(linear model),创建总模型(global model),即包括所有参数:
global.model <- lm(birdspp ~ area + isolation + plants + habitats, data = tilbird)然后利用glmulti包中的函数glmulti对所有可能模型中来选择最优模型。此处由于是4个参数,则共有2^4=16个可能模型(此处不考虑交互效应)。
bird.model <- glmulti(global.model, level = 1, crit = "aicc") #选用AICc进行评判模型###Initialization...
###TASK: Exhaustive screening of candidate set.
###Fitting...
###Completed.
summary(bird.model)###$name
###[1] "glmulti.analysis"
###
###$method
###[1] "h"
###
###$fitting
###[1] "lm"
###
###$crit
###[1] "aicc"
###
###$level
###[1] 1
###
###$marginality
###[1] FALSE
###
###$confsetsize
###[1] 100
###
###$bestic
###[1] 223.7
###
###$icvalues
### [1] 223.7 223.8 225.0 225.7 226.2 226.7 228.6 228.7 243.6 244.1 244.5
###[12] 244.5 246.0 246.7 246.8 247.0
###
###$bestmodel
###[1] "birdspp ~ 1 + area + habitats"
###
###$modelweights
### [1] 2.871e-01 2.708e-01 1.455e-01 1.049e-01 8.123e-02 6.348e-02 2.432e-02
### [8] 2.259e-02 1.332e-05 1.036e-05 8.538e-06 8.461e-06 3.984e-06 2.794e-06
###[15] 2.652e-06 2.496e-06
###
###$includeobjects
###[1] TRUE
结果出来了,最优模型只包括面积和生境的参数,看看:
lm9 <- lm(birdspp ~ area + habitats, data = tilbird)
summary(lm9)###
###Call:
###lm(formula = birdspp ~ area + habitats, data = tilbird)
###
###Residuals:
### Min 1Q Median 3Q Max
###-6.606 -2.107 -0.263 1.911 8.705
###
###Coefficients:
### Estimate Std. Error t value Pr(>|t|)
###(Intercept) 20.69295 2.08432 9.93 5.6e-12 ***
###area 0.01564 0.00289 5.41 3.9e-06 ***
###habitats 1.29893 0.55652 2.33 0.025 *
###---
###Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
###
###Residual standard error: 3.67 on 37 degrees of freedom
###Multiple R-squared: 0.474, Adjusted R-squared: 0.445
###F-statistic: 16.6 on 2 and 37 DF, p-value: 7e-06
但再看看刚才的模型的AICc结果:
summary(bird.model)$icvalue### [1] 223.7 223.8 225.0 225.7 226.2 226.7 228.6 228.7 243.6 244.1 244.5
###[12] 244.5 246.0 246.7 246.8 247.0
发现第二个模型的ΔAICc为223.8-223.7=0.1。坑爹啊!如果此时ΔAICc>2,则模型选择到此结束,即最优模型为第一个模型。可是,现实比较残忍,继续模型平均,列出所有可能模型:
lm1 <- lm(birdspp ~ area + isolation + plants + habitats, data = tilbird)
lm2 <- lm(birdspp ~ isolation + plants + habitats, data = tilbird)
lm3 <- lm(birdspp ~ area + plants + habitats, data = tilbird)
lm4 <- lm(birdspp ~ area + isolation + habitats, data = tilbird)
lm5 <- lm(birdspp ~ area + isolation + plants, data = tilbird)
lm6 <- lm(birdspp ~ plants + habitats, data = tilbird)
lm7 <- lm(birdspp ~ isolation + habitats, data = tilbird)
lm8 <- lm(birdspp ~ isolation + plants, data = tilbird)
lm9 <- lm(birdspp ~ area + habitats, data = tilbird)
lm10 <- lm(birdspp ~ area + plants, data = tilbird)
lm11 <- lm(birdspp ~ area + isolation, data = tilbird)
lm12 <- lm(birdspp ~ area, data = tilbird)
lm13 <- lm(birdspp ~ isolation, data = tilbird)
lm14 <- lm(birdspp ~ plants, data = tilbird)
lm15 <- lm(birdspp ~ habitats, data = tilbird)
lm16 <- lm(birdspp ~ 1, data = tilbird)看着比较壮观,但是碰到十个参数,共 2^10=1024 个可能模型的时候就比较麻烦了。没事,可以再编个程序循环一下就行,后文会再次提及此问题。
16个可能模型一起平均,
library(MuMIn)
lm.ave <- model.avg(lm1, lm2, lm3, lm4, lm5, lm6, lm7, lm8, lm9, lm10, lm11,
lm12, lm13, lm14, lm15, lm16)
summary(lm.ave)###
###Call:
###model.avg.default(object = lm1, lm2, lm3, lm4, lm5, lm6, lm7,
### lm8, lm9, lm10, lm11, lm12, lm13, lm14, lm15, lm16)
###
###Component models:
### df logLik AICc Delta Weight
###12 4 -107.3 223.7 0.00 0.29
###123 5 -106.0 223.8 0.12 0.27
###124 5 -106.6 225.0 1.36 0.15
###1234 6 -105.6 225.7 2.01 0.10
###13 4 -108.5 226.2 2.53 0.08
###1 3 -110.0 226.7 3.02 0.06
###134 5 -108.4 228.6 4.94 0.02
###14 4 -109.8 228.7 5.08 0.02
###3 3 -118.5 243.6 19.96 0.00
###23 4 -117.5 244.1 20.46 0.00
###(Null) 2 -120.1 244.5 20.85 0.00
###2 3 -118.9 244.5 20.86 0.00
###34 4 -118.4 246.0 22.37 0.00
###234 5 -117.5 246.7 23.08 0.00
###4 3 -120.1 246.8 23.18 0.00
###24 4 -118.9 247.0 23.31 0.00
###
###Term codes:
### area habitats isolation plants
### 1 2 3 4
###
###Model-averaged coefficients:
### Estimate Std. Error Adjusted SE z value Pr(>|z|)
###(Intercept) 22.023011 3.272613 3.327045 6.62 <2e-16 ***
###area 0.015423 0.002945 0.003044 5.07 <2e-16 ***
###habitats 1.287322 0.560392 0.579478 2.22 0.026 *
###isolation -0.001104 0.000728 0.000753 1.47 0.143
###plants 0.019405 0.021519 0.022247 0.87 0.383
###---
###Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
###
###Full model-averaged coefficients (with shrinkage):
### (Intercept) area habitats isolation plants
### 22.023011 0.015422 1.040595 -0.000531 0.005770
###
###Relative variable importance:
### area habitats isolation plants
### 1.00 0.81 0.48 0.30
结果中的第一部分,’Component models’,即列出了所有模型的自由度(df),对数似然函数(logLik),AICc值,ΔAICc值和模型权重。比如最优模型的模型权重为0.29,即为真实模型的可能性为29%(其实是非常低的,一般达到0.6-0.7就很不错了,当然,这里使用的数据是被我随机化过的,所以结果没有实际参考价值)
其中的第4部分,’Full model-averaged coefficients’,即是平均参数估计, $\hat{\bar{θ}}$ 。
第5部分,’Relative variable importance’,即是各个参数的重要值。最大为1,可见该例子中,面积是最重要的,次之是生境。至于隔离度和植物数量,则在模型中贡献不大。
MuMIn包里面其实有现成的命令dredge得到上述的部分结果,不信,试试输入以下一句命令:
dredge(global.model)此时如果打算计算各岛的预鸟类物种数,则可以如下进行模型平均:
pred.mat <- matrix(NA, ncol = 16, nrow = 40, dimnames = list(paste("isl", 1:40,
sep = ""), paste("lm", 1:16, sep = ""))) #建立一个空矩阵,放40个岛的各16各模型预测值,如下所示
pred.mat[, 1] <- predict(lm1)
pred.mat[, 2] <- predict(lm2)
pred.mat[, 3] <- predict(lm3)
pred.mat[, 4] <- predict(lm4)
pred.mat[, 5] <- predict(lm5)
pred.mat[, 6] <- predict(lm6)
pred.mat[, 7] <- predict(lm7)
pred.mat[, 8] <- predict(lm8)
pred.mat[, 9] <- predict(lm9)
pred.mat[, 10] <- predict(lm10)
pred.mat[, 11] <- predict(lm11)
pred.mat[, 12] <- predict(lm12)
pred.mat[, 13] <- predict(lm13)
pred.mat[, 14] <- predict(lm14)
pred.mat[, 15] <- predict(lm15)
pred.mat[, 16] <- predict(lm16)
##输出40个岛屿的平均预测值,即上述的 hat-bar(Y)
bird.pred <- pred.mat %*% summary(lm.ave)$msTable$weight[c(4,14,3,2,7,16,10,13,1,8,5,6,9,15,12,11)]
round(t(bird.pred),2) #把矩阵换方向,给页面省点空间,跟分析无关### isl1 isl2 isl3 isl4 isl5 isl6 isl7 isl8 isl9 isl10
###[1,] 44.76 30.01 26.82 25.98 25.85 24.97 24.87 29.67 26.19 25.46
### isl11 isl12 isl13 isl14 isl15 isl16 isl17 isl18 isl19 isl20
###[1,] 25.11 25.06 24.81 23.79 25.03 24.41 26 25.03 24.92 26.6
### isl21 isl22 isl23 isl24 isl25 isl26 isl27 isl28 isl29 isl30
###[1,] 25.63 25.12 24.32 24.1 25.02 24.62 24.15 26.52 27.03 23.69
### isl31 isl32 isl33 isl34 isl35 isl36 isl37 isl38 isl39 isl40
###[1,] 25.59 24.5 24.27 26.11 25.51 26.5 24.88 24.95 28.28 24.91
还有一点是非条件方差估计,这个,有点麻烦,等以后再说。计算方法其实跟上述的 $\hat{\bar{Y}}$ 类似。
实战演练二: 千岛湖墓群的决定因素
这个分析就跟上述方法相似了,按部就班:
tiltomb <- read.table("http://sixf.org/files/code/2014/tiltomb.txt", h = T) #读取墓的虚拟数据 'tiltomb.txt'
cor.sig(tiltomb[, -1])### area plants habitats SI elev convex
###area 1*** -0.139 -0.064 0.857*** 0.726*** 0.041
###plants -0.139 1*** -0.16 -0.167 -0.039 -0.107
###habitats -0.064 -0.16 1*** -0.034 -0.032 -0.187
###SI 0.857*** -0.167 -0.034 1*** 0.888*** 0.237
###elev 0.726*** -0.039 -0.032 0.888*** 1*** 0.307
###convex 0.041 -0.107 -0.187 0.237 0.307 1***
###slope 0.248 0.193 0.115 0.247 0.322* 0.264
###aspect -0.114 -0.081 0.141 0.069 0.278 0.075
###Al 0.088 -0.066 0.193 0.223 0.326* 0.06
###Si 0.055 -0.099 0.101 0.14 0.243 0.081
###sand -0.207 0.197 0.111 -0.22 -0.191 -0.311
###pH -0.194 -0.132 -0.204 -0.17 -0.228 0.018
### slope aspect Al Si sand pH
###area 0.248 -0.114 0.088 0.055 -0.207 -0.194
###plants 0.193 -0.081 -0.066 -0.099 0.197 -0.132
###habitats 0.115 0.141 0.193 0.101 0.111 -0.204
###SI 0.247 0.069 0.223 0.14 -0.22 -0.17
###elev 0.322* 0.278 0.326* 0.243 -0.191 -0.228
###convex 0.264 0.075 0.06 0.081 -0.311 0.018
###slope 1*** -0.093 0.412** 0.334* 0.111 -0.53***
###aspect -0.093 1*** 0.075 0.101 -0.086 0.198
###Al 0.412** 0.075 1*** 0.887*** 0.615*** -0.756***
###Si 0.334* 0.101 0.887*** 1*** 0.504*** -0.646***
###sand 0.111 -0.086 0.615*** 0.504*** 1*** -0.598***
###pH -0.53*** 0.198 -0.756*** -0.646*** -0.598*** 1***
结果发现面积、形状指数和海拔显著相关。考虑岛实际因素,岛屿面积或者说千岛湖以前的山头大小估计不会是墓葬考虑的因素,而这个山头圆不圆,这关乎风水的事,应该是主要因素,所以剔除面积和海拔。再看发现形状指数跟沙土也有正相关,可是考虑沙土多少是决定建不建墓的关键因素,予以保留,何况不是非常强烈的正相关(coef. = 0.373)。再看发现铝、硅和坡度有相关,可以确信铝和硅,其中之一是冗余的,因为白膏泥富含铝和硅。白膏泥相对铝含量较多,此处选择去除硅,以及另外的坡度。pH跟沙土相关,看来得把pH去除,估计过了上千年,墓葬中的有机质早化成泥土了。
再看看选取参数后的结果,
cor.sig(tiltomb[, c("plants", "habitats", "SI", "convex", "aspect", "Al", "sand")])### plants habitats SI convex aspect Al
###plants 1*** -0.16 -0.167 -0.107 -0.081 -0.066
###habitats -0.16 1*** -0.034 -0.187 0.141 0.193
###SI -0.167 -0.034 1*** 0.237 0.069 0.223
###convex -0.107 -0.187 0.237 1*** 0.075 0.06
###aspect -0.081 0.141 0.069 0.075 1*** 0.075
###Al -0.066 0.193 0.223 0.06 0.075 1***
###sand 0.197 0.111 -0.22 -0.311 -0.086 0.615***
### sand
###plants 0.197
###habitats 0.111
###SI -0.22
###convex -0.311
###aspect -0.086
###Al 0.615***
###sand 1***
后续步骤跟演练一类似,不同的是,此处的应变量为二元结构,即presence-absence数据,得用广义线性模型中的逻辑斯帝回归(logistic regression)。其他注解省略,直接上程序,
global.model.tomb <- glm(tomb ~ plants + habitats + SI + convex + aspect + Al +
sand, family = binomial("logit"), data = tiltomb)
tomb.model <- glmulti(global.model.tomb, level = 1, crit = "aicc")###Initialization...
###TASK: Exhaustive screening of candidate set.
###Fitting...
###
###After 50 models:
###Best model: tomb~1+SI
###Crit= 57.9820910321992
###Mean crit= 64.0858355584437

###
###After 100 models:
###Best model: tomb~1+SI
###Crit= 57.9820910321992
###Mean crit= 64.9421343165768

###
###After 150 models:
###Best model: tomb~1+SI
###Crit= 57.9820910321992
###Mean crit= 64.5619346833708

###Completed.
summary(tomb.model)###$name
###[1] "glmulti.analysis"
###
###$method
###[1] "h"
###
###$fitting
###[1] "glm"
###
###$crit
###[1] "aicc"
###
###$level
###[1] 1
###
###$marginality
###[1] FALSE
###
###$confsetsize
###[1] 100
###
###$bestic
###[1] 57.98
###
###$icvalues
### [1] 57.98 58.33 59.61 60.17 60.22 60.30 60.39 60.46 60.54 60.75 60.82
### [12] 60.94 62.15 62.17 62.18 62.24 62.39 62.44 62.67 62.70 62.77 62.77
### [23] 62.79 62.87 62.89 62.91 62.95 62.98 63.01 63.09 63.19 63.27 63.32
### [34] 63.51 63.53 63.60 63.66 64.05 64.43 64.52 64.53 64.60 64.62 64.77
### [45] 64.80 64.87 64.88 64.91 64.92 64.92 64.95 64.96 65.08 65.12 65.14
### [56] 65.40 65.40 65.45 65.52 65.54 65.58 65.65 65.66 65.67 65.69 65.69
### [67] 65.72 65.81 65.82 65.88 66.02 66.08 66.14 66.14 66.22 66.32 66.47
### [78] 66.56 66.64 66.72 66.82 66.85 66.91 66.92 66.93 67.22 67.35 67.37
### [89] 67.38 67.64 67.65 67.66 67.67 67.80 67.83 67.83 67.86 67.87 68.02
###[100] 68.17
###
###$bestmodel
###[1] "tomb ~ 1 + SI"
###
###$modelweights
### [1] 0.1201201 0.1011728 0.0531133 0.0401592 0.0392729 0.0377621 0.0359927
### [8] 0.0348480 0.0333513 0.0300502 0.0290503 0.0273379 0.0149678 0.0148350
### [15] 0.0147370 0.0143245 0.0132729 0.0129413 0.0115051 0.0113448 0.0109770
### [22] 0.0109687 0.0108420 0.0104403 0.0103423 0.0102346 0.0100197 0.0098576
### [29] 0.0097113 0.0093423 0.0088919 0.0085364 0.0083084 0.0075580 0.0074968
### [36] 0.0072460 0.0070090 0.0057865 0.0047700 0.0045613 0.0045489 0.0043911
### [43] 0.0043397 0.0040282 0.0039725 0.0038450 0.0038208 0.0037599 0.0037378
### [50] 0.0037365 0.0036946 0.0036696 0.0034468 0.0033923 0.0033552 0.0029419
### [57] 0.0029405 0.0028648 0.0027779 0.0027422 0.0026895 0.0025989 0.0025888
### [64] 0.0025730 0.0025506 0.0025475 0.0025079 0.0023998 0.0023883 0.0023173
### [71] 0.0021582 0.0020990 0.0020310 0.0020308 0.0019495 0.0018537 0.0017263
### [78] 0.0016468 0.0015814 0.0015211 0.0014462 0.0014228 0.0013853 0.0013789
### [85] 0.0013704 0.0011849 0.0011078 0.0011006 0.0010928 0.0009612 0.0009542
### [92] 0.0009487 0.0009451 0.0008861 0.0008726 0.0008723 0.0008583 0.0008546
### [99] 0.0007955 0.0007370
###
###$includeobjects
###[1] TRUE
结果一看,最优模型只包括形状指数,看来理论想像的数据也不错嘛,虽然烦人的ΔAICc依旧小于2,因此还得继续模型平均了。因为 2^7=128 个可能模型,手动输入运算则是比较折腾了,所以得写个循环程序让电脑来运算。
tomb7=tiltomb[, c("plants", "habitats", "SI", "convex", "aspect", "Al", "sand","tomb")]
npar=7
modPar=c("plants", "habitats", "SI", "convex", "aspect", "Al", "sand","tomb")
unit=c(1,0)
parEst=rep(unit,each=2^(npar-1))
for (i in 2:npar){
unit=c(i,0)
parEst.tmp=rep(rep(unit,each=2^(npar-i)),2^(i-1))
parEst=cbind(parEst,parEst.tmp)
}
parMat=cbind(parEst[,1:npar],1)
dimnames(parMat)=list(1:(2^npar),modPar)
allModel=list()
for (i in 1:(dim(parMat)[1]-1)) {
tomb7.tmp=tomb7[,parMat[i,]!=0]
allModel[[i]]=glm(tomb~.,family = binomial("logit"),data=tomb7.tmp)
}
modelC=glm(tomb~1,family = binomial("logit"),data=tomb7)
lm.ave <- model.avg(allModel,modelC)
summary(lm.ave)其中128个模型平均后的部分结果为:
### Full model-averaged coefficients (with shrinkage):
### (Intercept) SI Al sand aspect habitats convex plants
### -2.96791424 0.01986124 -0.09423029 -0.08413135 0.00217080 -0.04294219 0.00446755 0.00043138
###
###Relative variable importance:
### SI aspect Al sand habitats convex plants
### 0.98 0.27 0.27 0.26 0.24 0.23 0.22
再次放个大招吧,一次性列出模型平均后的部分结果:
dredge(global.model.tomb)结果
千岛湖鸟类多样性主要取决于岛屿面积和生境多样性,而墓葬可能性取决于岛屿的形状指数。
讨论
听说统计上有一个更牛的利器是随机森林模型(random forest model),可以无视参数是否独立,直接进入模型而且可以精确预测。哪天有兴趣琢磨琢磨。
PS: 以下是娱乐时间。
圆山头是墓葬的首选,所以,各位看官以后到千岛湖旅游,不要去什么猴岛蛇岛,选择山头比较圆的岛,才是王道!
最后检验一下鸟类多样性跟墓葬出现的相关性分析:
cor.test(tilbird[, 1], tiltomb[, 1])###
### Pearson's product-moment correlation
###
###data: tilbird[, 1] and tiltomb[, 1]
###t = 3.256, df = 38, p-value = 0.002378
###alternative hypothesis: true correlation is not equal to 0
###95 percent confidence interval:
### 0.1821 0.6797
###sample estimates:
### cor
###0.4671
结果是显著正相关(t = 3.2562, df = 38, p-value = 0.002378)。墓葬的出现,表示该岛风水还不错,所以最后证实本文的最初假设,即跟蜘蛛侠讨论时所做的预测:鸟类多样性与风水有显著的相关性。至于机理等科学问题的讨论,不是本篇论文能够解决的。请听下回分解。
致谢
谢谢看官的一路捧场,浏览完这块又长又臭的博文。谢谢实验室提供的平台和提供的支助,给于了我想像的空间,以及岛屿的数据。有关墓葬的生境数据,来自古田山大样地,我想像着搬到千岛湖了,在此一并致谢。分析方法部分参考于此。本文的源代码及数据可以点击此处(已更新)或此处(已过期)下载。看官就是reviewer(评审员),若有任何reviews,请尽请留言,谢谢!
参考文献
- Anderson, David R. (2008) Model based inference in the life sciences: a primer on evidence. New York: Springer.
- Burnham, Kenneth P. and David R. Anderson. (2002) Model selection and multimodel inference: a practical information-theoretic approach. Springer.
- Symonds, Matthew RE and Adnan Moussalli. (2011) A brief guide to model selection, multimodel inference and model averaging in behavioural ecology using Akaike’s information criterion. Behavioral Ecology and Sociobiology, 65: 13-21. APA
- Whittingham, Mark J. et al. (2006) Why do we still use stepwise modelling in ecology and behaviour?. Journal of Animal Ecology, 75: 1182-1189.
本文引用格式: Si X., Pimm S.L., Russell G.J. & P. Ding. (2014) Turnover of breeding bird communities on islands in an inundated lake. Journal of Biogeography, 41, 2283–2292.